株式会社QunaSysの大宮(インターン)・中川・高、大阪大学の水上渉准教授（QunaSys技術顧問）、三菱ケミカル株式会社の高玘上席主幹研究員と小林高雄主席研究員は、「状態平均軌道最適化変分量子固有値ソルバー(SA-OO-VQE)」という、量子コンピュータを用いて分子の複数の状態のエネルギーをバランス良く計算するアルゴリズムを発展させ、エネルギーの解析的な微分値を計算する手法を開発しました。さらに、開発した手法に基づいて計算されたエネルギーの微分値を、理論的解析が容易ではない円錐交差という点を含んだ光化学反応の反応経路を探索する問題に適用するデモンストレーションを行いました。円錐交差を含んだ化学反応経路を変分量子アルゴリズムを用いて求めた世界初の成果です。この成果は、アメリカ化学会の査読付き専門誌 Journal of Chemical Theory and Computation に掲載されました。

"Analytical Energy Gradient for State-Averaged Orbital-Optimized Variational Quantum Eigensolvers and Its Application to a Photochemical Reaction",
Keita Omiya*, Yuya O. Nakagawa*, Sho Koh, Wataru Mizukami, Qi Gao, and Takao Kobayashi,
https://doi.org/10.1021/acs.jctc.1c00877
(プレプリント版：https://arxiv.org/abs/2107.12705)

背景

近年、量子コンピュータの開発と研究が精力的に行われています。特に、現在実現しつつある、中規模かつ誤り訂正機能がないNISQ (Noisy Intermediate-Scale Quantum)デバイスと呼ばれる種類の量子コンピュータは、特定のタスクにおいて既存の古典コンピュータを上回る性能を持つことが期待されています[1]。NISQデバイスはノイズの影響を受けるため、実行できるのは比較的単純な数種類のアルゴリズムのみですが、その中でも変分量子固有値ソルバー(VQE; variational quantum eigensolver)と呼ばれるアルゴリズムが最も注目を集めています[2]。VQEは、分子や物質のエネルギーを量子力学に基づいて計算するための手法で、量子コンピュータと古典コンピュータをうまく組み合わせることで、NISQデバイス上でも動作が容易になるような工夫がなされています。

VQEを用いた分子のエネルギー計算をさらに実用に近づけるために、QunaSysを含む複数のグループによって、軌道最適化VQE（OO-VQE)という手法が提案されました[3]。OO-VQEは、そのままでは多数の量子ビットが必要になるような大規模な計算を、少数の量子ビットを持つ量子コンピュータを活用して扱う手法です。OO-VQEはさらに状態平均(state-average)というテクニックと組み合わせて拡張され、状態平均OO-VQE(SA-OO-VQE)という手法が提案されました[4]。SA-OO-VQEは、分子の基底状態（最安定状態）と励起状態のエネルギーを小さな量子コンピュータを用いてバランス良く求める手法として、様々な化学計算への応用が期待されています。

問題点

エネルギーは物質の静的な性質を決定する基本的な量ですが、動的な性質、例えば化学反応がどのように起こるのか、を知ることも非常に重要です。動的な性質を調べるための最も基本的な量の一つが、物質の状況（パラメータ）を少し変化させた時にエネルギーがどれくらい変化するのか、つまりエネルギーの微分値です。例えば、分子の原子核が少し動いたときにエネルギーがどの程度変化するのかがわかれば、分子がどのように動くのかを知ることができます。
前述したSA-OO-VQEでは、エネルギーの値そのものは計算できるものの、その解析的な微分値を求める手法は知られていませんでした。ノイズを含み、計算結果に揺らぎがあるNISQデバイスにおいては、有限の数値差分を用いた微分値の計算は精度面に問題があると考えられるため、解析的な微分値を計算するアルゴリズムの開発は非常に重要です。

手法・結果

本研究では、古典コンピュータを用いた化学計算で用いられてきたラグランジアン法という手法に基づき、SA-OO-VQEでのエネルギーの解析的な微分値の計算式を導出しました。そして、NISQデバイス上で簡単に測定ができる量を適切に組み合わせることで、SA-OO-VQEによって得られるエネルギーの解析的な微分値が計算できることを示しました。
さらに、この手法の有用性をデモンストレーションするために、円錐交差という理論的解析が容易ではない点を含み、典型的かつ重要な光化学反応であるシス-トランス光異性化を示すようなモデル分子(図1)に対して、SA-OO-VQEによるエネルギーとその微分値を計算しました。得られたエネルギーとその微分値を、既存の化学反応経路探索手法のサブルーチンとして用いた結果、古典コンピュータでの対応手法である状態平均CASSCF法を用いた結果と遜色ない反応経路が求まることを確認しました(図2・図3)。この結果から、SA-OO-VQEを用いたエネルギーとその微分値の計算が、実際の光化学反応の解析に適用できることが例証されました。

なお、本研究の数値計算は、理想的な量子コンピュータの動作を古典コンピュータを用いてシミュレートすることで行われ、SA-OO-VQEによるエネルギーとその微分値は、QunaSysが開発・有償提供している汎用量子化学計算ソフトウェアQamuyによって計算されました。

展望

本研究により、SA-OO-VQEという量子コンピュータを活用した高精度な計算手法において、エネルギーの微分値という基本的な量が計算できるようになりました。エネルギー微分値は、化学反応の解析など計算化学において頻用される量であるため、本研究で開発されたアルゴリズムはNISQデバイスの応用先をさらに広げていくことが期待されます。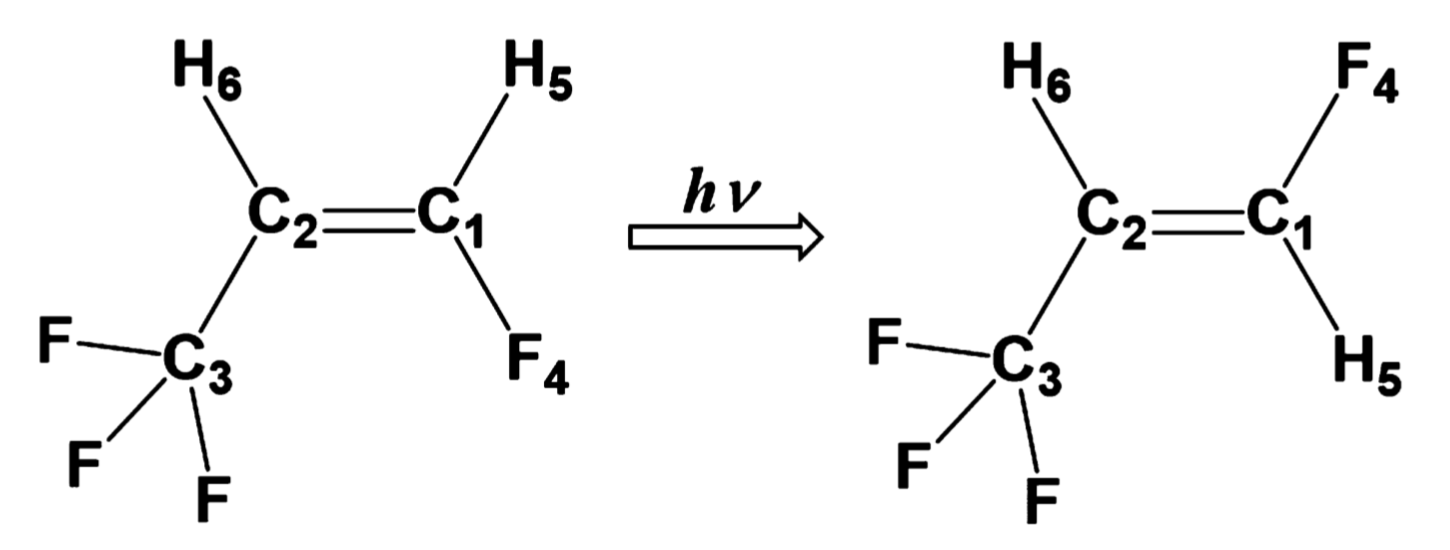


図1:円錐交差を含んだシス-トランス光異性化の反応経路探索に用いたモデル分子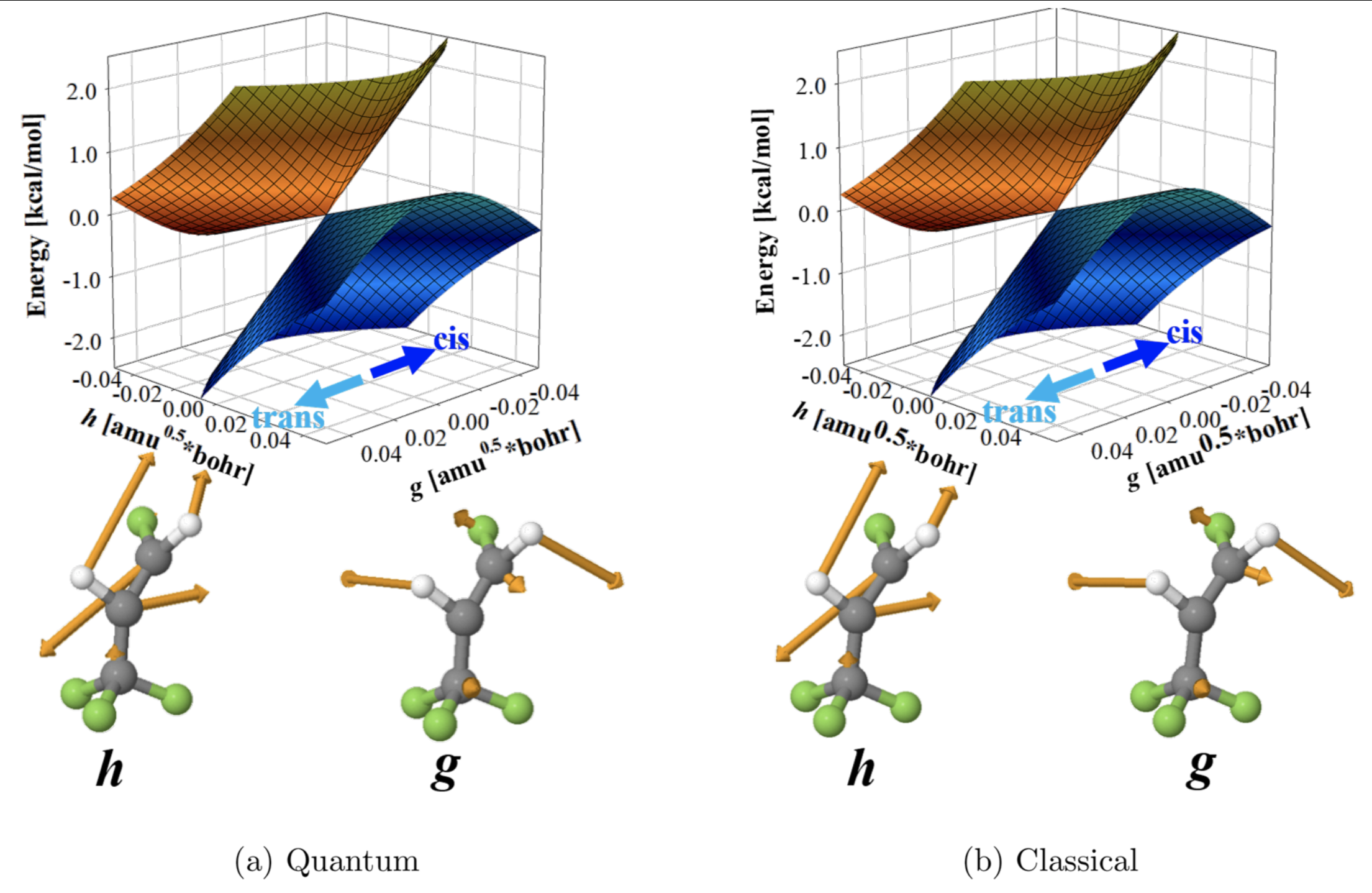




図2: 光異性化に関わる2つのエネルギー準位が交差する円錐交差周辺のポテンシャルエネルギー曲面の計算結果。左がSA-OO-VQEを用いた結果で、右が古典コンピュータの対応手法であるSA-CASSCF法を用いた結果。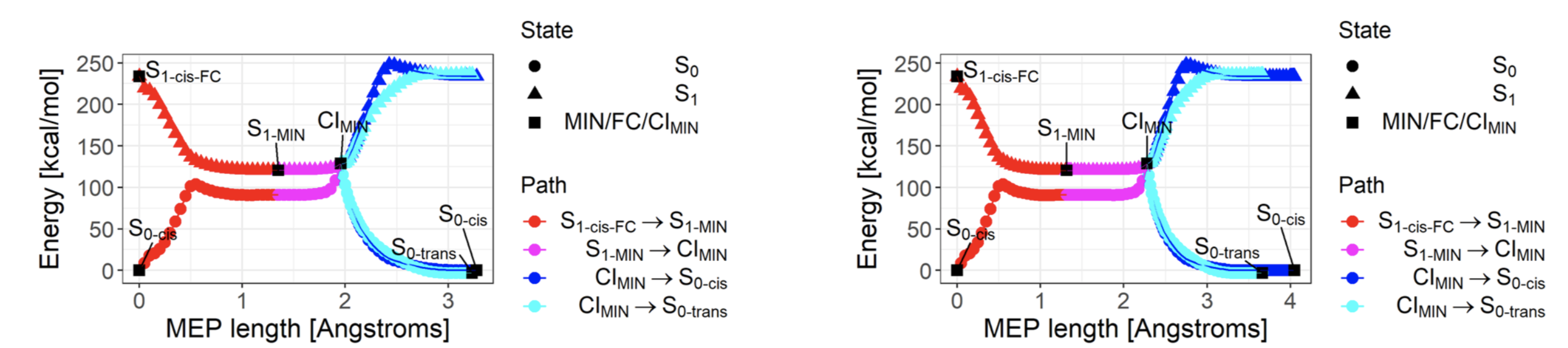




図3: 光異性化の反応経路に沿ってエネルギーをプロットした図。左がSA-OO-VQEを用いた結果で、右が古典コンピュータの対応手法であるSA-CASSCF法を用いた結果。

参考文献

[1] https://www.qmedia.jp/google-supremacy-1/
[2]  A. Peruzzo et al., Nat. Commun. 5, 4213 (2014) https://www.nature.com/articles/ncomms5213
[3] T. Takeshita et al., Phys. Rev. X 10, 011004 (2020)
https://journals.aps.org/prx/abstract/10.1103/PhysRevX.10.011004,
I. O. Sokolov et al., J. Chem. Phys. 152, 124107 (2020), https://aip.scitation.org/doi/10.1063/1.5141835,
W. Mizukami et al., Phys. Rev. Research 2, 033421 (2020), 
https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.2.033421, 
[4] S. Yalouz et al., Quantum Sci. Technol. 6 024004 (2021),  https://iopscience.iop.org/article/10.1088/2058-9565/abd334